12.椭圆曲线密码

Elliptic Curve Cryptography，ECC，椭圆曲线密码 ，是利用椭圆曲线来实现密码技术的统称。虽然叫椭圆，但实际上椭圆曲线的图像并不是椭圆形的。椭圆曲线源自于求椭圆弧长的椭圆积分的反函数。一般情况下，椭圆曲线可用下列方程式表示，其中 a,b,c,d 为系数，a ≠0 ，ax³+bx²+cx+d=0 没有重根。

E: y²= ax³+bx²+cx+d

由于椭圆曲线方程中存在 y² 项，因此椭圆曲线必然关于 x 轴对称。

椭圆曲线通常是指由魏尔斯特拉斯方程 y² = x³ + ax + b （其中 4a³ + 27b² ≠ 0 ，以确保曲线非奇异）所定义的平面代数曲线。

比特币使用的数字签名算法为椭圆曲线DSA，其中使用的椭圆曲线方程为 x²=y³+7 。

例如，当 a = 1 ， b = 0 ，c = -2 ，d = 4 时，所得到的椭圆曲线为：

E₁: y² = x³-2x+4

此椭圆曲线 E₁ 的图像如下所示，根本不是椭圆形：

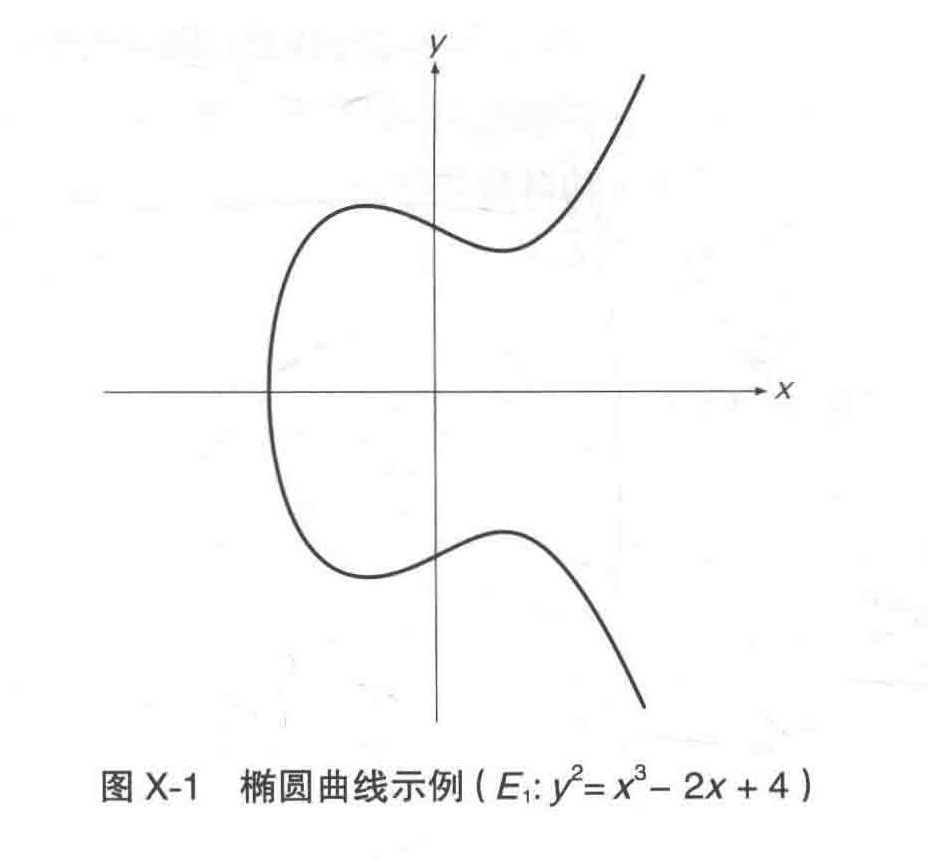
椭圆曲线密码包括以下内容：

• 基于椭圆曲线的公钥密码
• 基于椭圆曲线的数字签名
• 基于椭圆曲线的密钥交换

在SSL/TLS中使用了椭圆曲线Diffie-Hellman密钥交换（ECDH、ECDHE）和椭圆曲线DSA（ECDSA）；比特币也使用了椭圆曲线DSA。

椭圆曲线密码可以用比RSA更短的密钥来实现同等强度， 椭圆曲线密码密钥短但强度高 。例如密钥长度为224~255比特的椭圆曲线密码，与密钥长度为2048比特的RSA具有几乎相等的强度。

椭圆曲线运算

加法

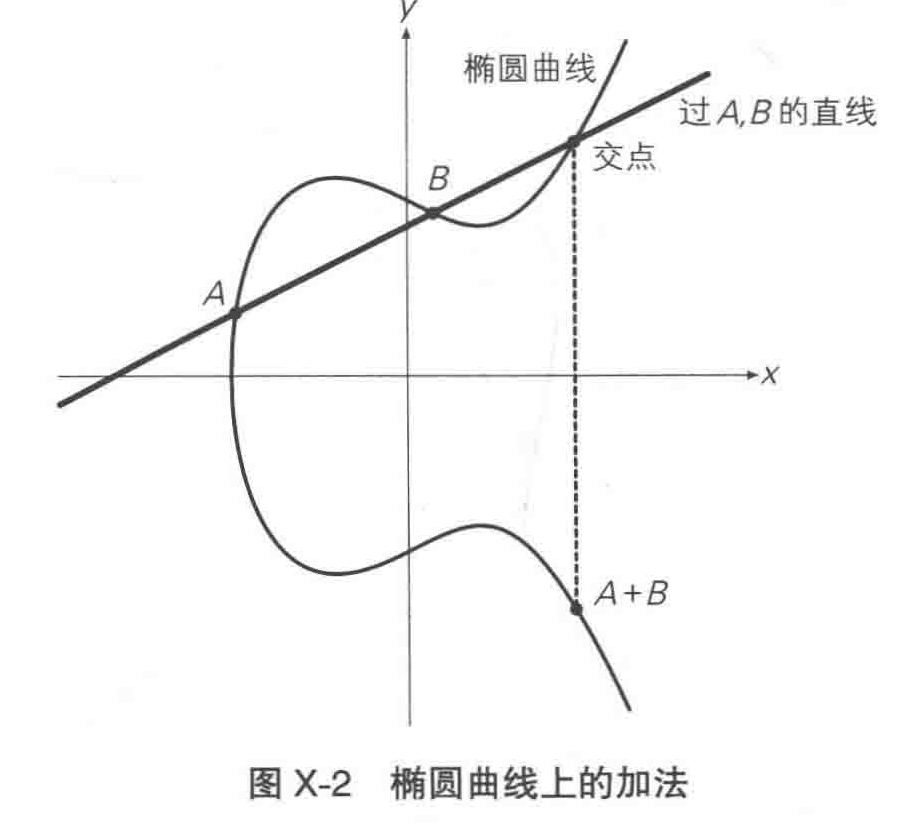
曲线上过两点 A，B 画一条直线，找到直线与椭圆曲线的交点，该交点关于 x 轴对称位置的点被定义为 A + B 。

二倍运算、正负取反运算

在加法运算中，若 A 与 B 重合，则无法画出【过两点的直线】。此时，如下图所示，我们画出【曲线在点 A 的切线】，然后找到该切线与椭圆曲线的交点，将该交点关于 x 轴对称位置的点定义为 A + A ，也就是 2A 。这样的运算成为【椭圆曲线上的二倍运算】。

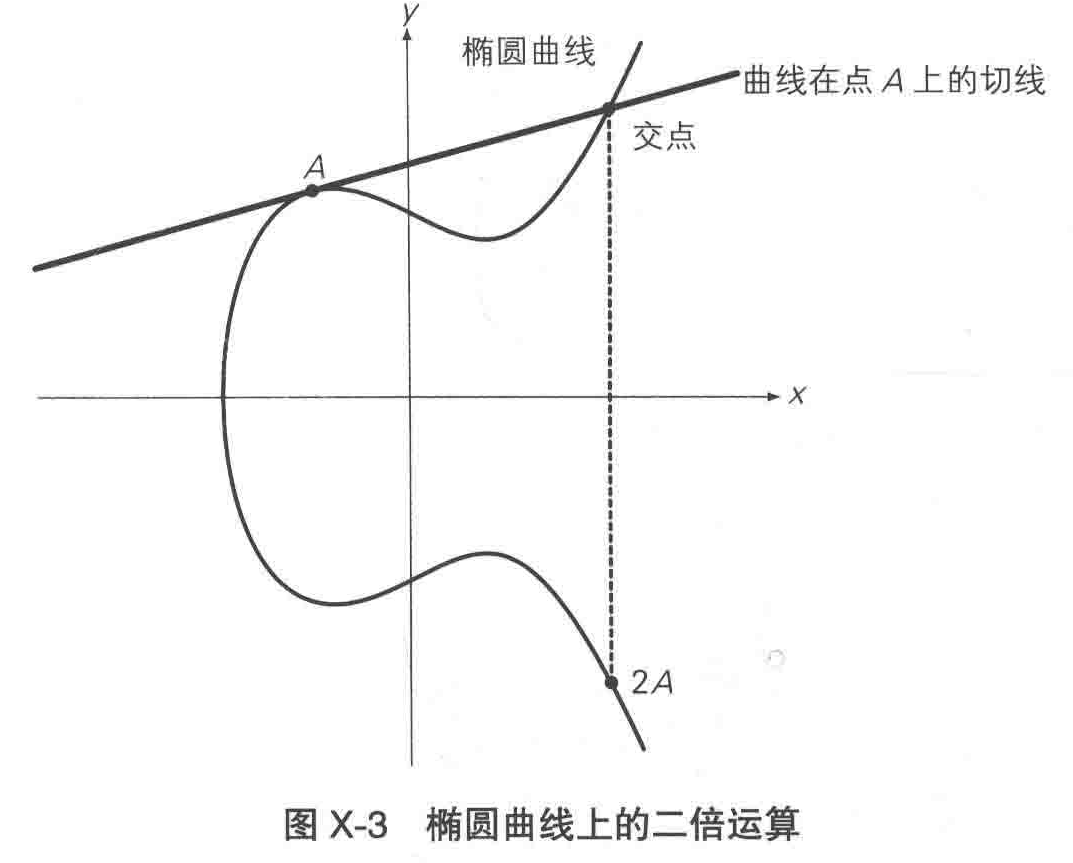
此外，点 A 关于 x 轴对称位置的点被定义为 -A。这样的运算称为【椭圆曲线上的正负取反运算】。

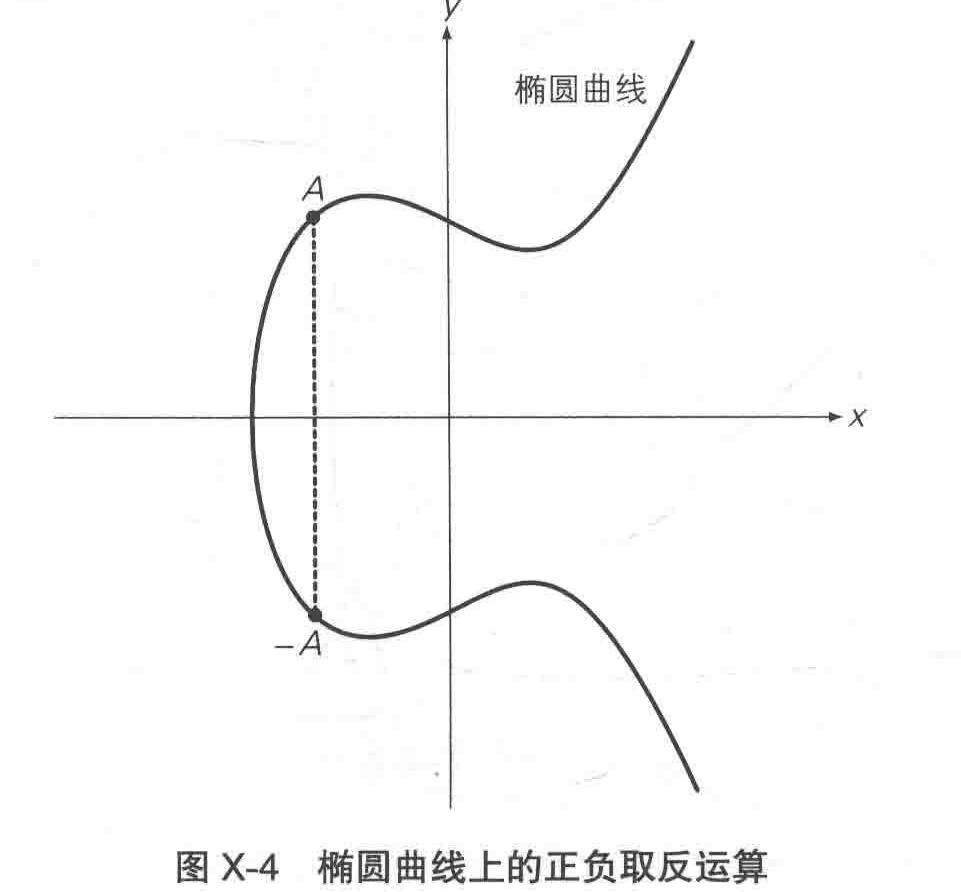
如果将 A 和 -A 相加会怎样呢？

根据椭圆曲线加法的定义，我们应该找到过点A和-A的直线与椭圆曲线的交点，但 A 与 -A 关于 x 轴对称，于是我们认为这条直线与椭圆曲线在【无限远点】的位置相交。这个无限远点在图像上画不出来，我们将其记作 O 。无限远点 O 的作用和数字 0 相近，A + (-A)=O 是永远成立的。

在椭圆曲线密码中， O 用于表示无限远点，因此在椭圆曲线的图像上一般不会在原点处标 O 。

基于上述运算规则，给定椭圆曲线上的某一点 G ，我们就可以求出 2G 、3G 等点的坐标。2G 相当于 G 的二倍；3G 相当于 G + 2G 。也就是说，当给定点 G 时，【已知数 x 求点 xG 的问题】并不困难，但反过来，【已知点 xG 求数 x 的问题】则非常困难。这就是椭圆曲线密码中所利用的【椭圆曲线上的离散对数问题】。

椭圆曲线上的离散对数问题

Elliptic Curve Discrete Logarithm Problem ，ECDLP，本质就是【已知点 xG 求数 x 的问题】。

• 已知

  • 椭圆曲线 E
  • 椭圆曲线 E 上的一个点 G （基点）
  • 椭圆曲线 E 上的一个点 xG （G 的 x 倍）

• 求

  • 数 x

有限域上的椭圆曲线运算

椭圆曲线密码所使用的椭圆曲线并非在实数域 R 上，而是在有限域 F_p 上。

有限域 F_p 是指，对于某个给定的质数 p ，由 0,1,···,p-1 共 p 个元素组成的整数集合中定义的加减乘除运算。

此章只讲到了特征数为质数 p 的素域 GF(p)，椭圆曲线密码中还可以使用特征数为 2^m 的扩张域 GF(2^m)。

有限域中的运算就是前面章节提到的时钟运算（取余数）。

以下实例：

E₂:y² = x³ + x +1

当这个椭圆曲线 E₂ 位于实数域 R 上时，其图像如下图所示，是一条光滑的曲线：

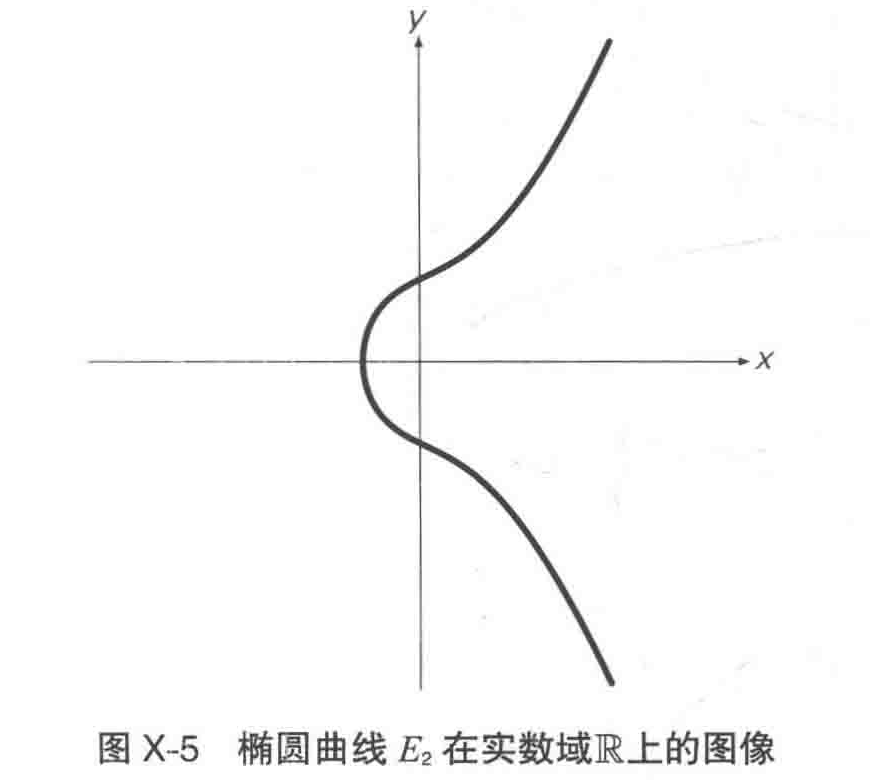
同样是这条椭圆曲线 E₂ ，当位于有限域 F₂₃ 上时，写作：

E₂:y² = x³ + x +1 (mod 23)

即左侧 y² 与右侧 x³ + x +1 的结果除以23的余数相等，这与时钟运算中以23为模的情况是一样的。

在有限域 F₂₃ 上的椭圆曲线图像如下图所示：

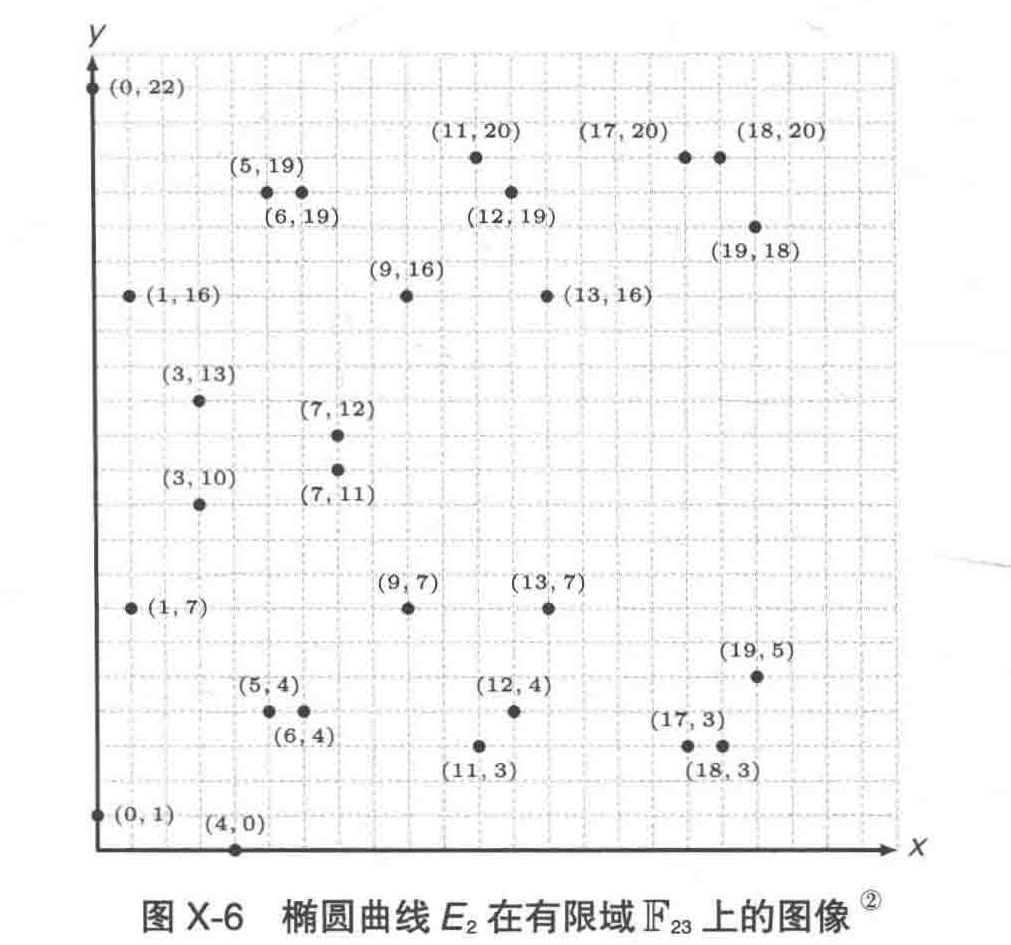
上图中，x，y 都只能取0到23之间的整数，因此图像并不是一条曲线，而是一些不连续的点。图中每个点的坐标(x,y)都满足【 y² 除以23的余数】等于【x³ + x +1 除以23的余数】。

如果我们以椭圆曲线 E₂ 上的点 G=(0,1)为基点，按照椭圆曲线【运算】的规则计算2G、3G、4G、5G、···，结果如下图所示：

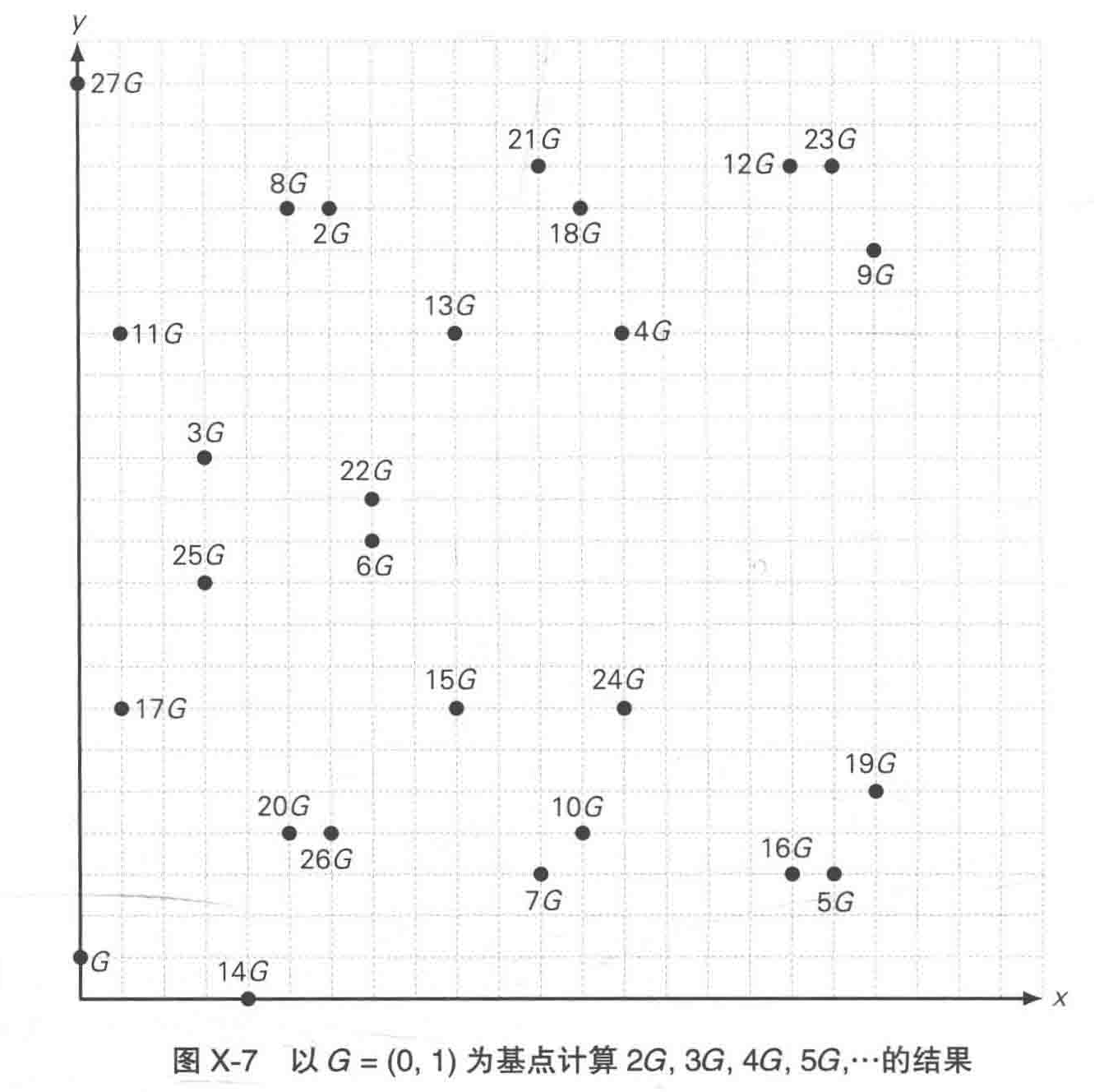
椭圆曲线上的离散对数问题，就是已知 G 和 xG 求 x 的问题。

举个例子，已知点 G=(0,1)，点 23G=(18,20)，求23。

这就是一个椭圆曲线上的离散对数问题。

当 p=23 是一个很小的数时，问题不太难解，但当 p 非常大时，要解这个问题是非常困难的。

以NIST推荐的一种椭圆曲线 Curve P-521 为例，其质数 p 是一个长达157位的数。

为了提高运算效率，NIST推荐使用梅森质数（或伪梅森质数），例如椭圆曲线 P-256 中，p=2²⁵⁶-2²²⁴+2¹⁹²+2⁹⁶-1。

• 椭圆曲线上的离散对数问题就是已知 G 和 xG 求 x
• 解椭圆曲线上的离散对数问题是非常困难的

椭圆曲线Diffie-Hellman密钥交换

非椭圆曲线的Diffie-Hellman密钥交换所利用的是：

• 以 p 为模，已知 G 和 G^x mod p ，求 x 的复杂度（有限域上的离散对数问题）

相对的，椭圆曲线Diffie-Hellman密钥交换所利用的则是：

• 在椭圆曲线上，已知 G 和 xG 求 x 的复杂度（椭圆曲线上的离散对数问题）

假设Alice和Bob需要共享一个对称密码的密钥，然而双方之间的通信线路已经倍窃听。此时，Alice和Bob可以通过以下方法进行椭圆曲线Diffie-Hellman密钥交换，从而生成共享密钥：

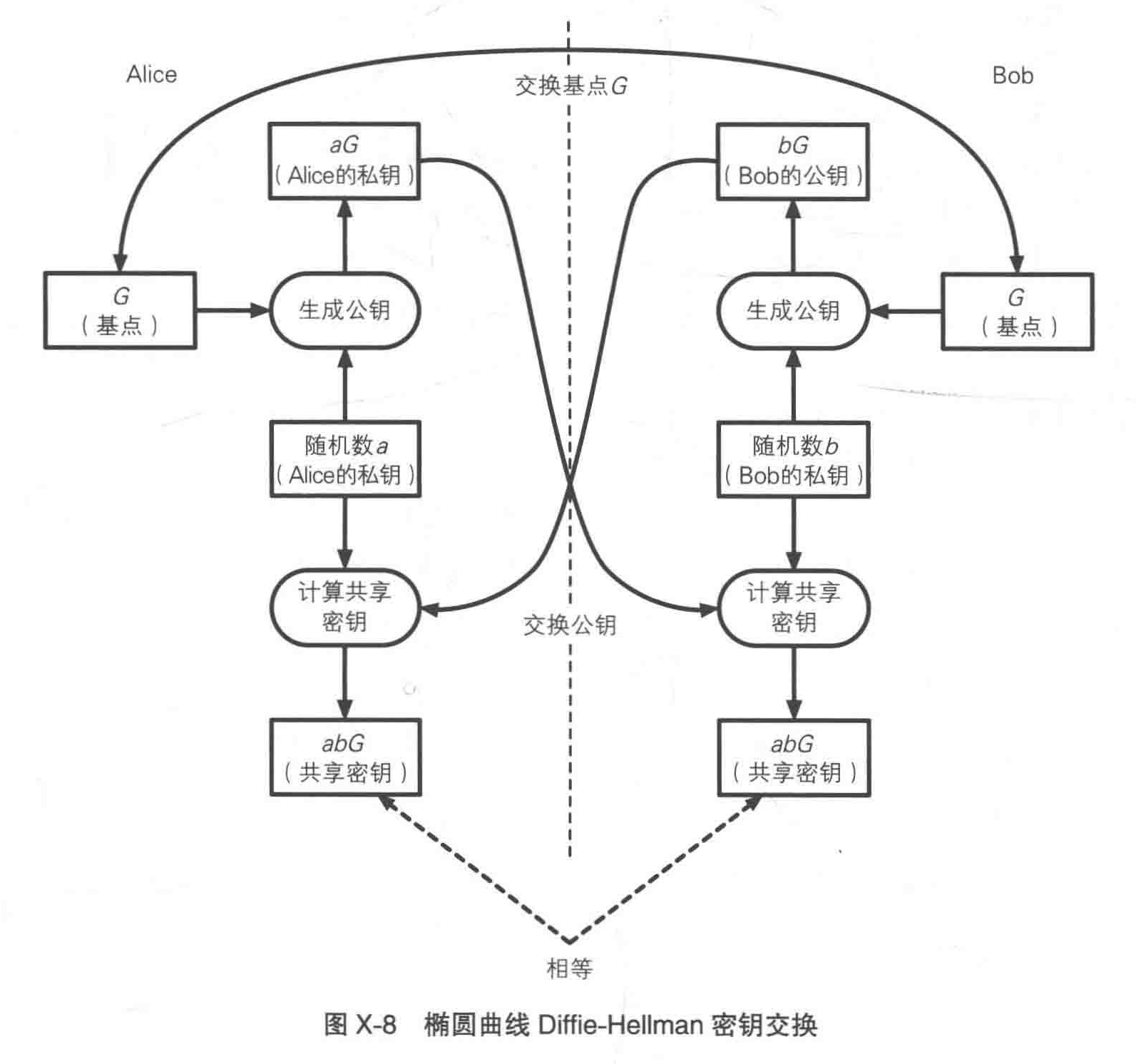
窃听者能够窃听的信息一共有3个：G 、aG 、bG ，但他无法求出 a 和 b ，也就无法计算出 abG 。

严格来说，椭圆曲线上的离散对数问题的复杂度只能证明【已知 G，aG，bG 难以求出 a，b 】，但无法证明【难以求出 abG】这需要另外证明

而Alice和Bob各自持有私钥 a 和 b ，因此双方能够根据 G 、aG 、bG 计算出 abG 。

Alice的计算方法为 a(bG)=abG ，而Bob的计算方法为 b(aG)=baG=abG 。经过这些步骤，Alice和Bob都生成了共享密钥 abG ，而窃听者却无法获取它。

综上所述，椭圆曲线Diffie-Hellman密钥交换正是基于椭圆曲线上的离散对数问题的复杂度来实现的。

在椭圆曲线Diffie-Hellman密钥交换中，生成共享密钥需要使用随机数 a 和 b 。如果每次通信都使用不同的随机数，则共享密钥也会随之改变，这样一来，即使在某个时间点通信的机密性被破解，由于每次通信使用的共享密钥不同，从而不必担心在此之前的通信内容被破解。这种特性称为 前向安全性 （Forward Secrecy，FS）或者 完全前向安全性 （Perfect Forward Secrecy，PFS）。

在SSL/TLS中使用椭圆曲线密码时，如果选择ECDHE_ECDSA和ECDHE_RSA密钥交换算法，就可以获得前向安全性。

ECDHE的意思是在Elliptic Curve Diffie-Hellman密钥交换中使用Ephemeral（短命的）密钥。

椭圆曲线ElGamal密码

利用通过椭圆曲线Diffie-Hellman密钥交换生成的密钥 abG ，可以很容易地实现椭圆曲线ElGamal密码。

假设Alice要向Bob发送一条消息，Alice可以将自己要发送的消息用椭圆曲线上的一个点 M 来表示（实际上使用的是该点的x坐标）。

加密

1. Alice用自己的私钥 a 以及Bob的公钥 bG ，对消息 M 计算点 M + abG 。此点即密文
2. Alice将密文 M + abG 发送给Bob

解密

3. Bob接收到密文 M + abG
4. Bob利用Alice的公钥 aG 以及自己的私钥 b 计算出共享密钥 abG
5. Bob将收到的密文 M + abG 减去共享密钥 abG 得到消息 M

由于窃听者无法计算出 abG ，因此即便窃取到密文 M + abG ，也无法计算出消息 M 。

椭圆曲线DSA（ECDSA）

使用椭圆曲线密码还可以实现数字签名。

假设Alice要对消息 m 加上数字签名，而Bob需要验证改签名。以下写着【计算】的部分都代表以 p 为模的时钟运算。

生成数字签名

1. Alice根据随机数 r 和基点 G 求出点 rG=(x,y)
2. Alice根据随机数 r 、消息 m 的散列值 h 、私钥 a 计算 s=(h+ax)/r
3. 最后，Alice将消息 m 、点 rG=(x,y) 和 s 发送给Bob，其中点 rG 和 s 就是数字签名

验证数字签名

4. Bob接收到消息 m 、点 rG=(x,y) 和 s

5. Bob根据消息 m 求出散列值 h

6. 最后，Bob根据上述信息，用Alice的公钥进行以下计算

   (h/s)G+(x/s)(aG)

   并将结果与 rG 进行比较。

   如果数字签名正确，则计算结果应该如下所示：

   

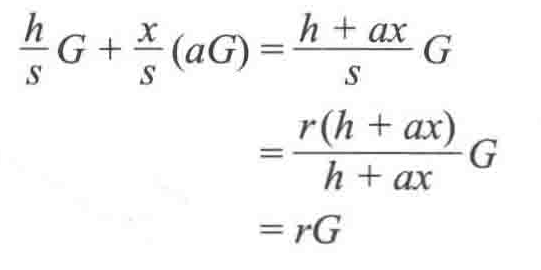
   由于攻击者没有Alice的私钥 a ，因此无法计算出合法的 s 。此外，即便是对于同一条消息，只要改变随机数 r ，所得到的数字签名也会随之改变。